Bloom Filter是一种空间效率很高的随机数据结构,它利用位数组很简洁地表示一个集合,并能判断一个元素是否属于这个集合。Bloom Filter的这种高效是有一定代价的:在判断一个元素是否属于某个集合时,有可能会把不属于这个集合的元素误认为属于这个集合(false positive)。通常应用在一些需要快速判断某个元素是否属于集合,但是并不严格要求100%正确的场合。而在能容忍低错误率的应用场合下,Bloom Filter通过极少的错误换取了存储空间的极大节省。
集合表示和元素查询
下面我们具体来看Bloom Filter是如何用位数组表示集合的。初始状态时,Bloom Filter是一个包含m位的位数组,每一位都置为0。
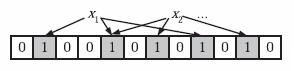
为了表达S={x1,x2,…,xn}这样一个n个元素的集合,Bloom Filter使用k个相互独立的哈希函数(Hash Function),它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x,第i个哈希函数映射的位置hi(x)就会被置为1(1≤i≤k)。注意,如果一个位置多次被置为1,那么只有第一次会起作用,后面几次将没有任何效果。在下图中,k=3,且有两个哈希函数选中同一个位置(从左边数第五位)。
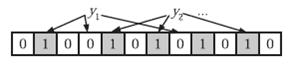
在判断y是否属于这个集合时,我们对y应用k次哈希函数,如果所有hi(y)的位置都是1(1≤i≤k),那么我们就认为y是集合中的元素,否则就认为y不是集合中的元素。下图中y1就不是集合中的元素。y2或者属于这个集合,或者刚好是一个false positive。
错误率估计
前面我们已经提到了,Bloom Filter在判断一个元素是否属于它表示的集合时会有一定的错误率(false positive rate),下面我们就来估计错误率的大小。在估计之前为了简化模型,我们假设kn<m且各个哈希函数是完全随机的。当集合S={x1,x2,…,xn}的所有元素都被k个哈希函数映射到m位的位数组中时,这个位数组中某一位还是0的概率是:
p′=(1−1m)kn≈e−knm
其中1m表示任意一个哈希函数选中这一位的概率(前提是哈希函数是完全随机的),(1−1m)表示哈希一次没有选中这一位的概率。要把S完全映射到位数组中,需要做kn次哈希。某一位还是0意味着kn次哈希都没有选中它,因此这个概率就是(1−1m)kn。令 p′=e−knm是为了简化运算,这里用到了计算e时常用的近似:
limx→∞(1−1x)−x=e
令ρ为位数组中0的比例,则ρ的数学期望E(ρ)=p′。在ρ已知的情况下,要求的错误率(false positive rate)为:
(1−ρ)k≈(1−p′)k≈(1−p)k
(1−ρ)为位数组中1的比例,(1−ρ)k就表示k次哈希都刚好选中1的区域,即false positive rate。上式中第二步近似在前面已经提到了,现在来看第一步近似。p′只是ρ的数学期望,在实际中ρ的值有可能偏离它的数学期望值。M. Mitzenmacher 已经证明[2] ,位数组中0的比例非常集中地分布在它的数学期望值的附近。因此,第一步的近似得以成立。分别将p和p′代入上式中,得:
f′=(1−(1−1m)kn)k=(1−p′)k
f=(1−e−knm)k=(1−p)k
相比p′ 和f′,使用p和f通常在分析中更为方便。
最优的哈希函数个数
既然Bloom Filter要靠多个哈希函数将集合映射到位数组中,那么应该选择几个哈希函数才能使元素查询时的错误率降到最低呢?这里有两个互斥的理由:如果哈希函数的个数多,那么在对一个不属于集合的元素进行查询时得到0的概率就大;但另一方面,如果哈希函数的个数少,那么位数组中的0就多。为了得到最优的哈希函数个数,我们需要根据上一小节中的错误率公式进行计算。
先用p和f进行计算。注意到f=ekln(1−e−knm),我们令g=kln(1−e−knm),只要让g取到最小,f自然也取到最小。由于p=e−knm,我们可以将g写成
g=−mnln(p)ln(1−p)
根据对称性法则可以很容易看出当p=12,也就是k=ln(2)mn时,g取得最小值。在这种情况下,最小错误率f等于12k≈(0.6185)mn。另外,注意到p是位数组中某一位仍是0的概率,所以p=12对应着位数组中0和1各一半。换句话说,要想保持错误率低,最好让位数组有一半还空着。
需要强调的一点是,p=12时错误率最小这个结果并不依赖于近似值p和f。同样对于f′=ekln(1−(1−1m)kn),g′=kln(1−(1−1m)kn),p′=(1−1m)kn,我们可以将g′写成
g′=1nln(1−1m)ln(p′)ln(1−p′)
同样根据对称性法则可以得到当p′=12时,g′取得最小值。
位数组的大小
下面我们来看看,在不超过一定错误率的情况下,Bloom Filter至少需要多少位才能表示全集中任意n个元素的集合。假设全集中共有u个元素,允许的最大错误率为є,下面我们来求位数组的位数m。
假设X为全集中任取n个元素的集合,F(X)是表示X的位数组。那么对于集合X中任意一个元素x,在s=F(X)中查询x都能得到肯定的结果,即s能够接受x。显然,由于Bloom Filter引入了错误,s能够接受的不仅仅是X中的元素,它还能够є(u−n)个false positive。因此,对于一个确定的位数组来说,它能够接受总共n+є(u−n)个元素。在n+є(u−n)个元素中,s真正表示的只有其中n个,所以一个确定的位数组可以表示
个集合。m位的位数组共有2m个不同的组合,进而可以推出,m位的位数组可以表示
个集合。全集中n个元素的集合总共有
个,因此要让m位的位数组能够表示所有n个元素的集合,必须有
即:
上式中的近似前提是n和єu相比很小,这也是实际情况中常常发生的。根据上式,我们得出结论:在错误率不大于є的情况下,m至少要等于nlog2(1/є)才能表示任意n个元素的集合。
上一小节中我们曾算出当k=ln2·mn时错误率f最小,这时f=12k=12mln2n。现在令f≤є,可以推出
这个结果比前面我们算得的下界nlog2(1/є)大了log2e≈1.44倍。这说明在哈希函数的个数取到最优时,要让错误率不超过є,m至少需要取到最小值的1.44倍。
算法实现
下面给出一个简单的Bloom Filter的实现代码:
1 | import java.util.BitSet; |
总结
在计算机科学中,我们常常会碰到时间换空间或者空间换时间的情况,即为了达到某一个方面的最优而牺牲另一个方面。Bloom Filter在时间空间这两个因素之外又引入了另一个因素:错误率。在使用Bloom Filter判断一个元素是否属于某个集合时,会有一定的错误率。也就是说,有可能把不属于这个集合的元素误认为属于这个集合(False Positive),但不会把属于这个集合的元素误认为不属于这个集合(False Negative)。在增加了错误率这个因素之后,Bloom Filter通过允许少量的错误来节省大量的存储空间。
自从Burton Bloom在70年代提出Bloom Filter之后,Bloom Filter就被广泛用于拼写检查和数据库系统中。近一二十年,伴随着网络的普及和发展,Bloom Filter在网络领域获得了新生,各种Bloom Filter变种和新的应用不断出现。可以预见,随着网络应用的不断深入,新的变种和应用将会继续出现,Bloom Filter必将获得更大的发展。


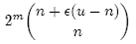
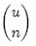
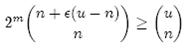
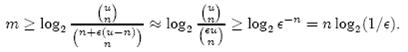
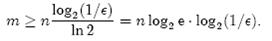



未找到相关的 Issues 进行评论
请联系 @gouyuwang 初始化创建